General Mathematics: Functions

 

General Mathematics is one of the core subjects of Senior High School Students. In the earlier part of this subject, functions will be introduced. 

In a real-life setting, some people might say it is not commonly being observed. It is not true. In fact, it exists, we can't just notice it sometimes. Let's take the following for example.

Let's say you're working as a tutor. Now think about the income you will earn from it. Let's say you get 200 pesos for tutoring math. The amount of money you get, which is the output, will depend on the number of hours you tutored a particular student (input).

That example is just a simple function. It is not just about the money. The functions are used to figure out how things change.

What are functions?

Functions serve as a cornerstone for understanding the relationships between domains. 

To better understand its meaning, here's a comparison with it to relation.

Differentiate relation with function

Relation

It is any set of ordered pairs. 

Domain, or the first elements of ordered pairs, is the set of x-values. It is otherwise known as the input.

Range, or the second elements of ordered pairs, is the set of y-values. It is otherwise known as the output, which is dependent on the input.

Function
In its simplest term, it is a relation where every element in the domain corresponds to only one value in the range. Each value of x relates to only one value of y.

Important Keynote: one-to-one relationship

Examples:

x: 1 2 3 4 5
y: 6 12 18 24 30

1 relates to 6; 2 relates to 12; and so on. No values of y have the same values of x.

z = {(4,1), (3,9), (2,8), (7,5)}

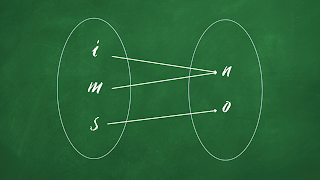
This one is a function, too, because each value of x relates exactly to only one value of y.

Using diagrams, we can also identify which is a function and which is just a mere relation.

The first one is a function since each element in the domain relates to a distinct element in the range. However, the second one is not a function but a mere relation because there is a value of x that relates to more than one value of y.

Remember: All functions are relations. However, a relation can only be a function if all the values of the domain (x) correspond to exactly one value of the range (y).

You just have read one lesson from the general mathematics subjects. It is actually one of my subjects back then, where I got one of my highest grades. If you have a hard time understanding this topic, try to repeat from reading it again. 

You may also supplement what you have learned by watching more examples on platforms where you can learn such as in Youtube. After which, try to solve several problems on your own.

It is just okay if you will still commit mistakes on the first few questions. Just repeat and repeat until you master this topic. As the saying goes, practice makes perfect, so take your time learning it. Do your best and focus so you can find the rationale behind it, and from then, you will have no problem in solving similar questions.

In case you are still having a hard time fully understanding it, then I suggest you should have some rest first because sometimes, if we're tired, we cannot think properly. Therefore, take a nap or go somewhere else and relax. After that, give your full attention again to understanding it, and it should be better already at that time. And if that's the case, celebrate small achievements by patting your shoulder and treating yourself with something.